JAVA - 거품정렬(Bubble Sort)
✅ 거품정렬 ( Bubble Sort )
알고리즘의 실행시간이 입력크기의 제곱에 비례하는 O(n^2)의 시간복잡도는 가지는 거품정렬은
구현이 간단한 정렬알고리즘이지만 속도가 느린편이며 선택정렬과 시간복잡도를 가지지만
데이터 교환횟수가 상대적으로 많다.
거품정렬은 데이터를 '비교' 하며 찾기때문에 '비교정렬'이며
정렬대상인 데이터외에 추가적인 공간을 필요로하지 않기때문에 '제자리정렬'이기도 하다.
데이터를 교환하는 과정에서 temp(임시변수)가 필요하긴하지만 적은양이기에 제자리정렬로 볼 수 있다.
📌 정렬과정
1. 초기데이터배열이 주어진다.
2. 제일 앞부터 해당원소와 다음원소를 비교한다.
3. 두 원소 중 현재원소가 다음원소의 값보다 더 크다면 두원소의 자리를 바꾼다.
4. 다음원소로 이동해 현재원소와 그 다음원소를 비교하며 끝가지 반복한다.

초기 데이터배열이 주어진다.

제일 앞부터 두 원소씩 비교한다.
1. 5와 7을 비교했지만 현재원소5가 다음원소7보다 크지않기때문에 자리교환이 발생하지 않았다.
2. 7과 3을 비교한결과 현재원소7이 다음원소3보다 크기때문에 자리교환이 발생해 53791 인 상태가되었다.
3. 53791인 배열에서 7,9를 비교했으나 자리교환이 발생하지 않았다.
4. 53791인 배열에서 9,1을 비교해 현재원소인 9가 더 크므로 자리교환이 발생했다
5. 이 결과 한바퀴 돌았을 때 제일 끝인덱스에 제일 큰값이 들어가 정렬된 상태로 볼 수 있다.

위에서 한바퀴를 돈 결과 데이터는 53719이 되었고 이 중 제일끝인덱스는 정렬이 된상태이므로 해당인덱스 전까지만 반복한다
1. 5와 3비교 자리교환 발생
2. 5와 7비교 자리교환 발생하지않음
3. 7과 1비교 자리교환 발생
4. 35179의 배열이 되었다.
5. 제일끝-1인덱스까지 정렬된상태로 볼 수 있다.
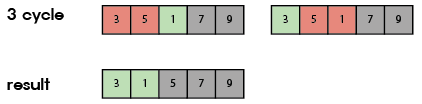
위의 과정에서 정렬된 인덱스들은 비교하지 않는다, 즉 반복될때마다 가장 끝에서부터 -1의 인덱스까지는 비교하지 않게되는 셈이다.

마지막에는 0과 1인덱스의 원소들만 남게되고 이 둘을 비교한 뒤 버블정렬은 끝나게된다.
🚩 각 사이클당 제일 끝 인덱스부터 한개씩 정렬되기때문에 사이클이 한번씩 추가될때마다 비교할 값이 줄어들게된다
총 사이클은 배열 크기 - 1 번 진행되며, 각 사이클별 비교횟수는 배열크기 - 사이클횟수 만큼 비교하게된다.
📌 코드구현
package sort;
public class BubbleSort {
public static void main(String[] args) {
int[] data = {5,7,3,9,1};
int temp=0; // 값변경을 위한 임시변수(그릇의 역할)
// 배열의 크기 - 1 만큼 진행하게하기위함
for(int i=1;i<data.length;i++) {
// 반복된 사이클만큼 덜 비교할 수 있게하기위해 -i
for(int j=0;j<data.length-i;j++) {
// 현재원소가 더 크다면 자리교환
if(data[j] > data[j+1]) {
temp = data[j];
data[j] = data[j+1];
data[j+1] = temp;
}
}
// 사이클별로 정렬된 배열 확인용
for(int x=0;x<data.length;x++) {
System.out.print(data[x]);
}
System.out.println();
}
}
}
🚩 자리교환하는 방식은 임시변수 temp를 선언해주고 if문의 조건에따라 현재원소가 더 크다면
temp에 현재원소data[j]의 값을 갖고있게하고 현재원소data[j]에 다음원소data[j+1]의 값을 넣고
다음원소data[j+1]는 temp가 갖고있던 data[j]였던 원소의 값을 받는 방식으로 교환이 발생한다.
출력결과

i를 0 부터 시작하고 j<data.length-1로 조건을 주어도 결과가 나오긴하지만
그렇게 구현할 경우 j가 계속 고정값인 data.length-1 전까지 비교하므로
위의 그림에서 설명한것처럼 정렬된 인덱스는 비교하지 않는다는 설명에 맞지않게된다.
따라서 i는 1부터 시작하도록하고 j의 조건은 data.length-i로 설정하는 편이 더 알맞다.
📌 거품정렬 정리
거품정렬알고리즘은 가장 기초적인 알고리즘이지만 비효율적 방식이므로 거의 사용되지 않는다.
또한 같은 시간복잡도O(n^2)를 갖는 삽입,선택정렬과 비교해보아도 교환이 더 많이 발생하므로 실질적으로 더 많은 시간이 걸리게된다.
🟢 장점
- 추가메모리 소비가 작다.
- 구현이 매우 간단하다.
- 안정정렬이 가능하다.
🔴 단점
- 다른 정렬 알고리즘들에 비해 교환과정이 많아 효율이 좋지 못하다.


-참고
https://st-lab.tistory.com/195?category=892973